Glosario de Comandos Maple

Me parecio interesante hacer un glosario con los comandos de Maple, porque muchas veces me pasa que necesito hacer algo y no tengo mucho tiempo para averiguar como se hace con el comando "?".

Si tienen más vayan posteándolos yo iré agregando también.

Asignación a variables: (:= , unassing, restore, assume)

var := comando maple;
Se evalua el comando maple y la expresión que resulta es asignada a la variable var

assume(x>a); assume(n,integer); assume(z,real)
Son ejemplos de assume. Para mayor información ejecute ?assume;

unassign('var');
Borra todo lo que se conoce acerca de la variable var, incluyendo las restricciones impuestas con el comando assume. De este modo, ella puede ser usada sin restricciones más adelante. Las comillas ' ' son fundamentales.

restore;
Reinicializa todas las variables que se hayan ocupado borrando todo lo que se conoce sobre ellas. Es equivalente a aplicar unassign('var') a cada variable var que se haya ocupado.

Aproximaciones decimales: (evalf)

Digits:= N;
Define que de ahora en adelante se ocupa aritmética decimal con N dígitos significativos. Al iniciar Maple Digits vale 10

evalf( expr);
Evalúa la expresión en artimética decimal con N dígitos sgniticativos, donde N es el valor que tiene la variable Digits.

evalf(expr,N);
Evalua la expresión expr en aritmética decimal con N dígitos significativos.

Álgebra: (expand, combine, simplify, factor, normal, coeff, quo, rem)

expand( expresion);
Expande la expresión desarrollando potencias de binomios, distribuyendo productos con sumas, o expandiendo fórmulas trigonométricas, etc.

combine( expresion);
Aplicado a ciertas expresiones realiza la operación inversa de expand

simplify(expresion);
Aplica las reglas de simplificación que cumplen las funciones típicas trigonométricas, exponenciación, logaritmos, polinomios, etc.. La noción que Maple tiene de una expresión simplificada es con toda probabilidad diferente de la que Ud. tiene, la que es a su vez diferente de la de su vecino.

factor(polinomio);
Factoriza el polinomio en factores con coeficientes enteros, racionales.

factor(polinomio,real);
Factoriza el polinomio en factores con coeficeintes reales usando aritmética de punto flotante.

factor(polinomio,complex);
Factoriza el polinomio en factores lineales complejos usando aritmética de punto flotante.

normal(expresion);
Obtiene una expresión en la forma denominador/numerador, con términos comunes simplificados.

coeff( expresion ,x^k);
Obtiene el coeficiente de x^k en la expresion, siempre que ésta sea una suma de pontencias de x.

q:= rem(a,b,x); r:= rem(a,b,x);
Si a,b son polinomios (en función de x), q es el cuociente de a dividido por b y r es el resto de a dividido por b. El resto y el couciente satisfacen a= b*q+r, donde grado® < grado (b)

Expresiones versus procedimientos: (->, proc(), subs(), unapply())

f:= x -> expr;
Define un procedimiento que asigna a cada x (input) su valor f(x) (output) que se obtiene al reemplazar el valor de x en la expresión expr

r:= expr;
Asigna a la variable r la expresión dada.

subs( {x=a},expr);
Retorna la expresión expr donde x es reemplazado por el valor de a.

subs( {x=a,y=b},expr);
Retorna la expresión expr donde x es reemplazado por el valor de a, y es reemplazado por el valor de b

subs( {eq1,eq2,.., eqk}, expresion);
Donde eq1, eq2, ... eqk, son reglas de substitución.

unapply(expr,x);
Retorna el procedimiento x->expr

Gráfico de funciones y curvas en el plano: (plot)

plot( f(x), x=a..b);
Grafica y=f(x) en el intervalo [a,b]. El rango y escala del eje Y se ajusta automáticamente

plot ( f(x) , x=a..b, scaling=constrained);
Igual que el anterior pero las escalas en los ejes X a Y están en relación 1:1.

plot ( f(x) , x=a..b, y=c..d);
Muestra la porción del gráfico de y=f(x) que yace en el rectángulo a <= x <= b, c<= y <= d.

plot( f(x), x=a..b, view=[x1..x2,y1..y2]);
Muestra la porción del gráfico de y=f(x) para a <= x <= b pero enmarcado en una ventana con x1 < x < x2, y1 < y < y2.

plot ( f(x) , x=a..b, y=c..d, discont=true);
Igual que el anterior, pero se usa cuando f es discontínua (y f no toma valores complejos)


plot( f(x), x=a..b, y=c..d, discont=true, color=COLOR);
Idem que el anterior donde y=f(x) se grafica con color COLOR, donde COLOR puede ser red, blue, green, cyan, magenta, etc...

plot( [f(x),g(x), h(x)] , x=a..b, y=c..d,discont=true, color=[red,blue,cyan]);
Idem que en el anterior pero se grafican las tres funciones f,g,h al mismo tiempo en colores red, blue, cyan respectivamente.

plot( [x(t), y(t) , t=a..b], color=red );
Grafica los puntos (x(t),y(t)) en el plano XY cuando t varía desde a hasta b.

plot( [x(t), y(t) , t=a..b], color=red, scaling=constrained) );
Igual que el anterior, pero las escalas en los ejes X,Y están en relación 1:1. (equivalente a presionar el botón 1:1 en la barra de menú del gráfico).

Más sobre gráficos: (with(plots), animate, display)

with(plots);
Activa al paquete plots donde se encuentran las rutinas, display, implicitplot, textplot, etc....

animate( { f(x), g(x,a)}, x=x1..x2, a=a1..a2, nframes);
Crea una animación donde en cada cuadro se grafica a las funciones f(x), g(x,a) en el intervalo [x1,x2], con a variando desde a1 hasta a2 con un incremento de 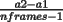. En total hay nframes cuadros.

p1:= plot( f(x), x=a..b):
Guarda en la variable p1 el gráfico de y=f(x), el cual puede ser desplegado mediante el comando display(p1). Note que la única manera en que el gráfico puede ser desplegado es mediante el comando display. Es conveniente terminar el comando con : en vez de ; para evitar ouput indeseable.

display(p1,p2,p3);
Grafica los gráficos guardados en las variables p1,p2,p3

display( sucesión o lista de de variables con gráficos, insequence=true);
Muestra cuadro a cuadro los gráficos en la lista creando una animación.

Solución de ecuaciones, sistemas de ecuaciones: (fsolve,solve)

fsolve( f(x)=g(x), x=a..b);
Calcula por métodos numéricos UNA solución de f(x)=g(x) en el intervalo [a,b], CON LA EXCEPCION del caso en que f(x), g(x) sean polinomios, donde encuentra TODAS las raices reales en el intervalo [a,b]

fsolve( f(x)=g(x), x=a);
Busca por métodos numéricos UNA solución de f(x)=g(x) comenzando la búsqueda en x=a. No necesariamente encuentra la solución más cercana a x=a.

fsolve( p(x),x);
Determina aproximaciones decimales a todas las raices reales del polinomio p(x).

fsolve( p(x),x,complex);
Determina aproximaciones decimales a todas las raices, incluyendo las complejas, del polinomio p(x)

solve( f(x)=g(x), x);
Si f, g son polinomios, encuentra todas las raices, en otros casos intenta encontrar tantas soluciones como pueda mediante reducciones algebraicas. Si no encuentra soluciones ya sea por que no hay o por que no pudo encontrar, retorna NULL, es decir "nada".

solve( f(x)< g(x), x);
Intenta resolver la inecuación mediante reducciones algebraicas (cálculo simbólico).

solve( conjunto de ecuaciones, conjunto de variables);
Intenta resolver mediante manipulaciones algebraicas el sistema de ecuaciones con respecto a las variables indicadas. Cuando tiene éxito, retorna una sucesión de reglas de substitución (para ser ocupadas con el comando subs).

CUIDADO: solve puede no encontrar todas las soluciones existentes de un sistema de ecuaciones no lineales.

Estructuras de datos, (expresión) sucesión, lista, conjunto, tabla: ([s], {s}, nops(s) , op(s) , seq(s) , s[n] , map(f,s))

Para agrupar varios datos en una misma variable, se puede usar una de las siguientes estructuras de datos: (expresión) sucesión, lista, conjunto, tabla.

exp1, exp2, ... , expn;
Es la sucesión formada por las expresiones exp1, exp2, etc. En general, expresiones separadas por comas definen a un sucesión. Las expresiones pueden ser de distintos tipos.

[s];
Es la lista formada por los elementos de la sucesión s. En general, si s es una sucesión entonces [s] es una lista.

{s};
Es el conjunto formado por los elementos de la sucesión s. En general, si s es una sucesión. entonces {s} es un conjunto. En maple un conjunto emula al concepto matemático de conjunto: elementos repetidos se eliminan y el orden de los elementos no importa.

T[algo]:=valor;
Si T no es una lista , crea la tabla T con una entrada. Con asignaciones adicionales del tipo T[indice]=valor se agregan elementos a la tabla T.

s[k];
El elemento k-ésimo de la lista o conjunto s.

T[algo];
Si T es una tabla, valor asociado a "algo" en la tabla.

nops(s);
El número de elementos de la lista o conjunto s.

op(s);
La sucesión con los elementos del conjunto o lista s (le quita los paréntesis a s)

seq( a(n), n=n1..n2 );
La sucesión a(n1), a(n1+1), a(n1+2), .... a(n2).

[ seq ( (a(n), n=n1..n2 ) ];
La lista con los elementos a(n1), a(n1+1), ... , a(n2)

{ seq ( (a(n), n=n1..n2 ) }
El conjunto con los elementos a(n1), a(n1+1), ... , a(n2). Elementos repetidos se eliminan.

map(f,s)
La lista o conjunto que se obtiene de aplicar una función f a cada elemento de la lista o conjunto s

Control de flujo: (for loops, while loops, if)

for i from n1 to n2 do BLO... od;
Ejecuta las instrucciones en el bloque BLO para i=n1, n1+1, etc.. hasta i=n2

for i from n1 to n2 by salto do BLO... od;
ejecuta las instrucciones en el bloque BLO para i=n1, n1+salto, etc.. hasta el mayor valor de n1+k*salto menor o igual a n2.

for k in S do BLO ... od;
Ejecuta las instucciones en el bloque BLO para cada elemento k en la lista o conjunto S.

while ( condicion) do BLO od:
Ejecuta las instucciones en el bloque BLO mientras la condición sea verdadera.

for k from n1 to n2 while ( condicion) do BLO od:
Ejecuta las instucciones en el bloque BLO mientras la condición sea verdadera y k esté entre n1 y n2 (inclusives)

if ( COND ) then BLOQUE fi
Si la condición COND es verdadera se ejecuta el BLOQUE.

if ( COND ) then BLOQUE1 else BLOQUE2 fi
Si la condición COND es verdadera se ejecuta el BLOQUE1, en caso contrario se ejecuta el BLOQUE2.

if ( COND ) then BLOQUE1 elif COND1 then BLOQUE2 else BLOQUE3 fi
Si la condición COND es verdadera se ejecuta el BLOQUE1 en caso contrario, si COND1 es verdadero se ejecuta el BLOQUE2, en otros casos se ejecuta BLOQUE3

Límites, límites por la izquierda y por la derecha: (limit())

limit(f(x),x=a,left);
Calcula el límite de f(x) cuando x tiende a "a" por la izquierda.

limit(f(x),x=a,right);
Calcula el límite de f(x) cuando x tiende a "a" por la derecha.

limit(f(x),x=a);
Calcula el límite cuando x tiende a "a", el cual existe sólo cuando 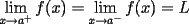. Si los límites por la izquierda o por derecha no existieran o no fueran iguales entonces el límite no existe y maple responde undefined

Derivadas: (D(), diff())

D(f);
Si f es una función entonces D(f) es la función f ' y entonces D(f)(x) es f '(x).

(D @@2) (f);
Si f es una función entonces (D@@2)(f) es la función f '', que es la segunda derivada de f .

diff(expr,x);
Si expr es una expresión en la variable x entonces diff(expr,x) es la derivada de expr con respecto a x.

diff( expr,x$2);
Es la segunda derivada de expr con respecto a la variable x.

diff( expr,x$3);
Es la tercera derivada de expr con respecto a la variable x.

diff( expr,x$n);
Es la n-ésima derivada de expr con respecto a la variable x.

Sumas de Riemann: (with(student), rightsum, leftsum, middlesum, trapezoid, leftbox, rightbox, middlebox)

with(student):
Activa al paquete de rutinas student. Se requiere para ocupar las rutinas que siguen.

leftsum(f(x), x=a..b,n);
Calcula la suma de Riemann para una partición de n subintervalos de igual longitud en que cada rectángulo tiene como altura el valor de la función en el extremo izquierdo de cada subintervalo. El valor de n es opcional. El valor por omisión es n=4.

rightsum( f(x), x=a..b,n);
Idem que el anterior pero para sumas derechas de Riemann.

middlesum( f(x), x=a..b,n);
Igual que el anterior pero para sumas de punto medio de Riemann.

trapezoid( f(x), x=a..b,n);
Estima 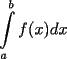mediante la fórmula trapezoidal para una partición uniforme de n subintervalos. Esto es, en vez de aproximar cada franja vertical por un rectángulo lo hace por el trapecio que une los puntos extremos de aquella.

leftbox( f(x), x=a..b, n);
Grafica los rectángulos correspondientes a la suma izquierda de Riemann de f(x) en el intervalo [a,b] para una partición de n subtintervalos de igual longitud (valor por omisión es n=4).

rightbox( f(x), x=a..b,n);
Idem que el anterior, pero para la suma derecha de Riemann

middlebox( f(x), x=a..b,n);
Igual que el anterior, pero para la suma en puntos medios de Riemann.

Integrales: (int(), Int(), evalf(Int ()), changevar, intparts)

int( f(x), x=a..b);
Intenta calcular 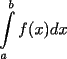mediante métodos simbólicos.

Int( f(x), x=a..b);
Es la expresión 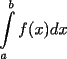NO EVALUADA. Es decir, es la expresión que al ser evaluada se obtiene la integral de f(x) en [a,b].

evalf ( Int (f(x),x=a..b);
Estima el valor de 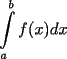mediante métodos numéricos (parecido a sumas de Riemann pero mucho más sofisticado y de alta precisión). Los límities de integración a,b deben ser números.

value( Int( f(x), x=a..b) );
Intenta evaluar mediante métodos simbólicos la integral de f(x) en el intervalo [a,b]. Es equivalente a int(f(x), x=a..b).

with(Student[Calculus1]): infolevel[Student[Calculus1]] := 1:
Se necesita para ejecutar los siguientes comandos ( se debió haber ejecutado antes with(student) ).

changevar(h(x)=g(u),expr,u);
Hace el cambio de variable a la función expr ( en la forma Int ), dejándola en función de u (antes estaba en función de x). Retorna la integral con el cambio de variable.

intparts(In,u(x));
Hace la integración por partes 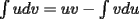. En el comando, In es la integral ( de la forma Int) y u(x) representa "u" en funcion de x. Retorna la integral con la integración por partes.